Ranking Loss

参考资料：https://blog.csdn.net/LoseInVain/article/details/103995962/

翻译自FesianXu， 2020/1/13, 原文链接 https://gombru.github.io/2019/04/03/ranking_loss/

ranking loss在很多不同的领域，任务和神经网络结构（比如siamese net或者Triplet net）中被广泛地应用。其广泛应用但缺乏对其命名标准化导致了其拥有很多其他别名，比如对比损失Contrastive loss，边缘损失Margin loss，铰链损失hinge loss和我们常见的三元组损失Triplet loss等。

1. 度量学习（Metric Learning）

一般的损失函数：
e.g. 交叉熵损失和均方差损失函数，这些损失的设计目的就是学习如何去直接地预测标签，或者回归出一个值，又或者是在给定输入的情况下预测出一组值，这是在传统的分类任务和回归任务中常用的。
ranking loss：
目的是去预测输入样本之间的相对距离。这个任务经常也被称之为度量学习(metric learning)。

在训练集上使用ranking loss函数是非常灵活的，我们只需要一个可以衡量数据点之间的相似度度量就可以使用这个损失函数了。
这个度量可以是二值的（相似/不相似）：比如，在一个人脸验证数据集上，我们可以度量某个两张脸是否属于同一个人（相似）或者不属于同一个人（不相似）。通过使用ranking loss函数，我们可以训练一个CNN网络去对这两张脸是否属于同一个人进行推断。（当然，这个度量也可以是连续的，比如余弦相似度。）

在使用ranking loss的过程中，

首先，从这两张（或者三张，见下文）输入数据中提取出特征，并且得到其各自的Embedding；

然后，我们定义一个距离度量函数用以度量这些表达之间的相似度，比如说欧式距离；

最终，我们训练这个特征提取器，以对于特定的样本对（sample pair）产生特定的相似度度量。

尽管我们并不需要关心这些表达的具体值是多少，只需要关心样本之间的距离是否足够接近或者足够远离，但是这种训练方法已经被证明是可以在不同的任务中都产生出足够强大的表征的。

2. ranking loss的表达式

Ranking loss主要针对以下两种不同的设置进行：

二元组的训练数据点（正例 + 负例）
三元组的训练数据点（Anchor + 正例 + 负例）

2.1 二元组的Loss

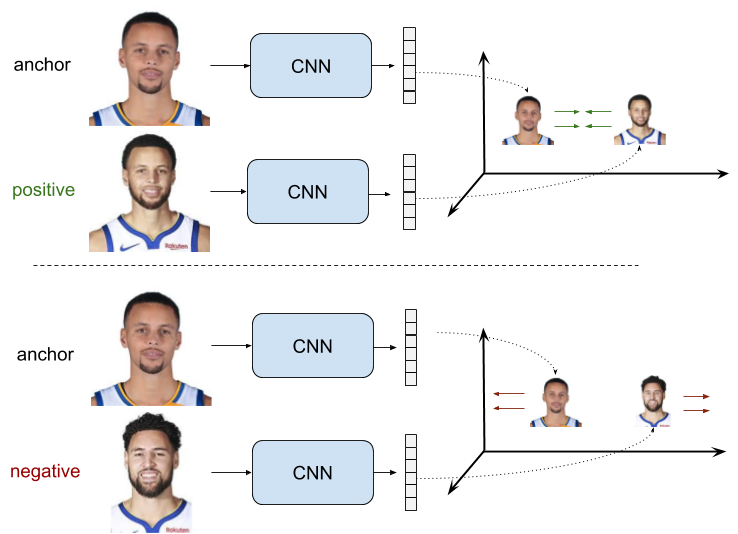
现在，我们的目标就是学习出一个特征表征，这个表征使得正样本对中的度量距离尽可能的小，而在负样本对中，这个距离应该要大于一个人为设定的超参数——阈值 $m$ 。

二元组的ranking loss的目标是：使正样本对中拥有趋向于0的度量距离；而在负样本对中距离至少大于阈值 $m$ 。

ra 表示anchor样本xa的特征
rp表示正样本xp的特征
rn表示负样本xn的特征

L=\left\{ \begin{align} d&(r_a,r_p)&& 正样本对(x_a,x_p)\\\\ m&ax(0,m-d(r_a,r_n))&&负样本对(x_a,x_n) \end{align} \right.

下面来解释一下这个Loss的意义：

对于正样本对来说，这个loss随着样本对输入到网络生成的表征之间的距离的减小而减少，增大而增大，直至变成0为止。
对于负样本来说，这个loss只有在所有负样本对的元素之间的表征的距离都大于阈值 $m$ 的时候才能变成0。
当实际负样本对的距离小于阈值的时候，这个loss就是个正值，因此网络的参数能够继续更新优化，以便产生更适合的表征。这个项的loss最大值不会超过 $m$ 。
设置阈值的目的：当某个负样本对中的表征足够好，xn与xa距离足够远的时候，就没有必要在该负样本对中浪费时间了，而是将训练会关注在其他更加难分别的样本对上。

假如用 $r_0,r_1$ 分别表示样本对两个元素的表征， $y$ 是一个二值数值：在输入的是负样本对时为0，正样本对时为1，用 $d(a,b)$ 表示两元素的距离，那么，上述的loss的函数表达式可以表示为：

L(r_0,r_1,y)=y*d(r_0,r_1)+(1-y)*max(0,m-d(r_0,r_1))

contrastive_loss（对比损失函数）

参考资料：https://blog.csdn.net/autocyz/article/details/53149760

我们来看在TensorFlow中，二元组的常用Loss——contrastive_loss。这种损失函数就是常用于孪生神经网络的。表达式与上述公式稍微有些出入，但是基本意思可是完全一样的。

L=\frac{1}{2N}\sum_{n=1}^N y*d^2+(1-y)*[max(0,m-d)]^2

$d$ 表示两个样本间的距离
$y$ 表示两个样本是否匹配：1表示匹配，0表示不匹配
$m$ 表示设定的阈值

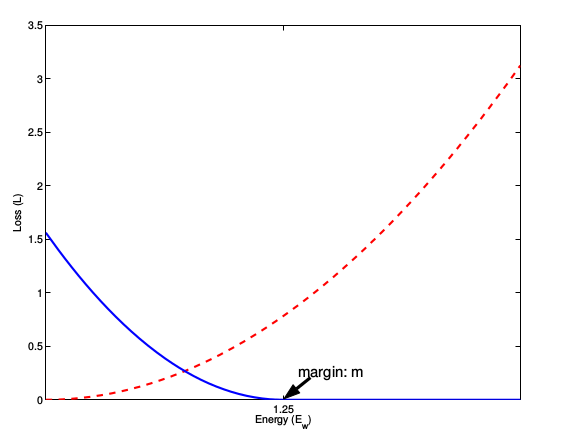
这张图表示的就是损失函数值与样本特征的欧式距离之间的关系：

红色虚线表示的是相似样本的损失值
蓝色实线表示的不相似样本的损失值

2.2 三元组的Loss

三元组样本对的Ranking Loss称为Triplet loss。最初是在 FaceNet: A Unified Embedding for Face Recognition and Clustering 论文中提出的，可以学到较好的人脸的embedding。

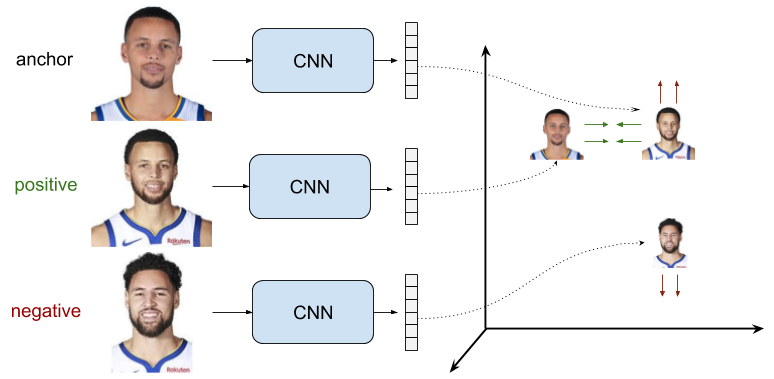
与二元组不同的是，输入样本对是一个从训练集中采样得到的三元组，这个也就是我们常说的L2R中的pairwise样式的数据形式。

Triplet Loss的训练目标是：锚点样本与负样本之间的距离 $d(r_a,r_n)$ 与锚点样本和正样本之间的距离 $d(ra,rp)$ 之差大于阈值 $m$ 。

这样可能说的比较绕，简单理解就是：让负样本原理锚点样本，正样本靠近锚点样本。

ra 表示anchor样本xa的特征
rp表示正样本xp的特征
rn表示负样本xn的特征

L(r_a,r_p,r_n)=max(0,m+d(r_a,r_p)-d(r_a,r_n))

这里，我们在训练过程中，需要注意对于采样需要非常注意，样本的采样好坏将直接影响到模型的效果。

我们可能遇到三种情况：

easy triplet： $d(r_a,r_n)>d(r_a,r_p) + m$ 。也就是说，比起正样本来说，负样本和锚点样本已经有足够的距离了（即是大于 $m$ ）。此时loss为0，网络参数将不会继续更新。
hard triplet： $d(r_a,r_n) < d(r_a,r_p)$ 。负样本比起正样本，更接近锚点样本，此时loss为正值（并且比 $m$ 大），网络可以继续更新。
semi-hard triplet： $d(r_a,r_p) < d(r_a,r_n)<d(r_a,r_p)+m$ 。负样本到锚点样本的距离比起正样本来说，虽然是大于后者，但是并没有大于设定的阈值 $m$ ，此时loss仍然为正值，但是小于 $m$ ，此时网络可以继续更新。

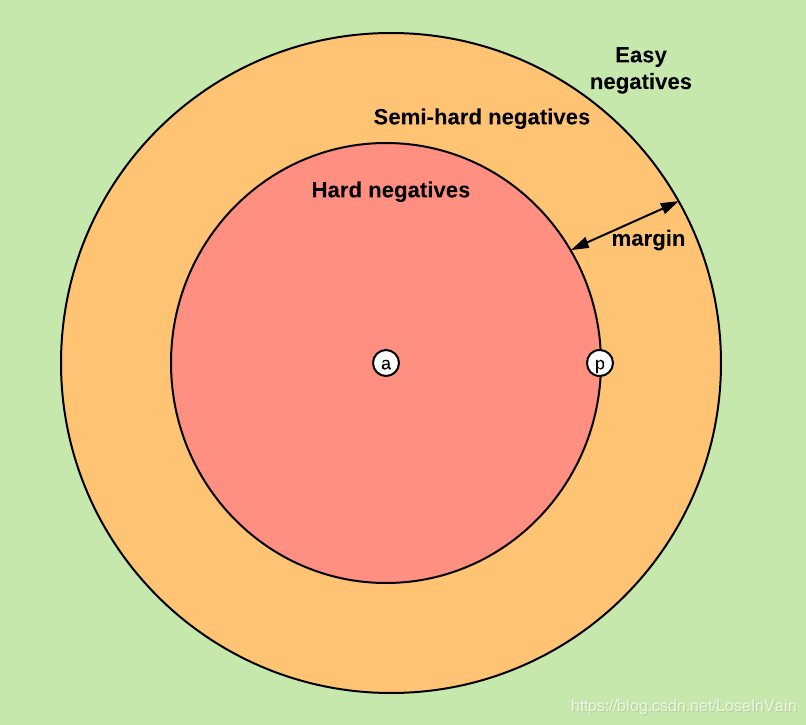
通过上面，我们可以看出，在构建负样本时，我们应该尽量避免采样到easy triplet，因为这样对于loss的共享为0，对优化没有什么作用。

因此，采样的策略是这样的：

参考资料：https://blog.csdn.net/u013082989/article/details/83537370

offline
online
- Batch All：
Batch Hard：
论文[《In Defense of the Triplet Loss for Person Re-Identification》]([1703.07737] In Defense of the Triplet Loss for Person Re-Identification)实验结果表明，batch hard的表现是最好的。

triplet_semihard_loss

最后更新于5年前

这有帮助吗？

1. 度量学习 （Metric Learning）