CRF

本部分主要整理从HMM-MEMM-CRF的知识点内容，旨在梳理在CRF中涉及到的重要相关知识点，从整体对概率图模型的有一个比较完善的认知。

参考资料：https://anxiang1836.github.io/2019/11/05/NLP_From_HMM_to_CRF/

问题1：HMM做了什么假设？

HMM具有2个强假设：

• 1阶齐次马尔科夫

  1阶：任意时刻的状态只依赖前一时刻的状态，与其他时刻无关

  齐次：链中任意节点间的转移所服从的概率分布都是相同的

• 观测独立假设

  任意时刻的观测只依赖于该时刻的状态，与其他状态无关。

问题2：HMM与MEMM的区别于关系？

HMM为隐马尔科夫模型，MEMM为最大熵马尔科夫模型。

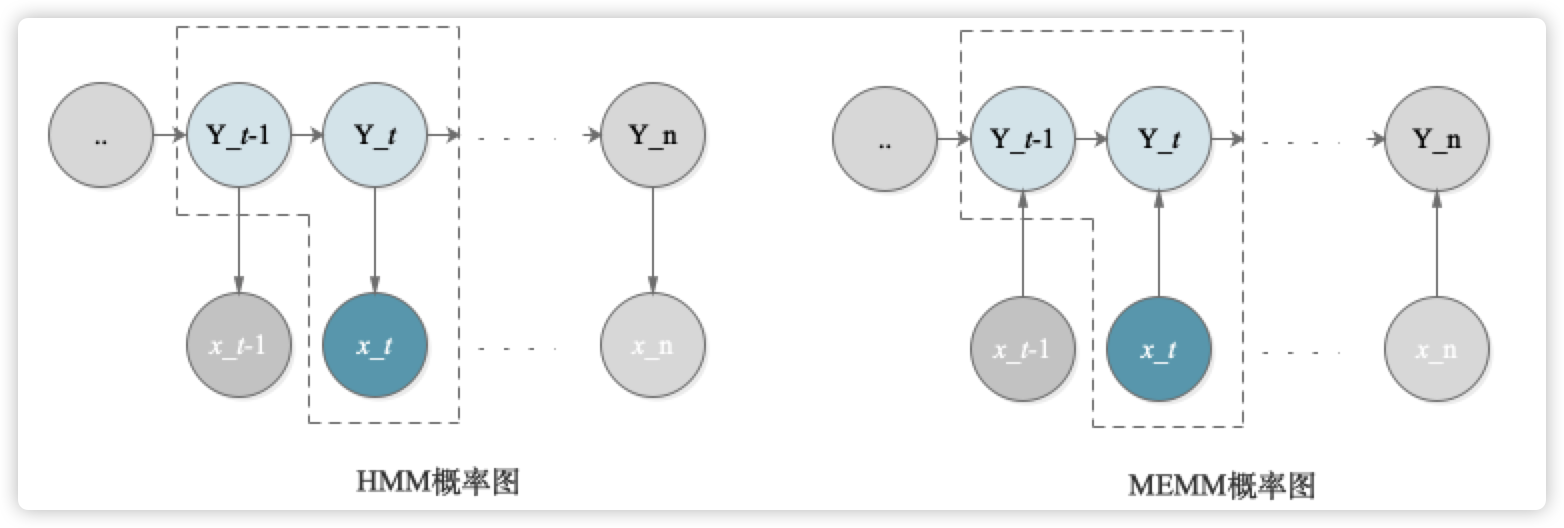
1. 从建模对象来看：

   HMM是概率生成模型，即是对P(X,Y)进行建模的；

   $$\begin{align} P(X,Y|\lambda) &= \prod_{t=1}^{T} P(x_t,y_t|\lambda)\\ &= \prod_{t=1}^{T} P(y_t|y_{t-1},\lambda) \bullet P(x_t|y_t,\lambda) \end{align}$$

   MEMM是概率判别模型，即是对P(Y|X)进行建模的；

   $$P(Y|X,\lambda)=\prod_{t=1}^T P(y_t|y_{t-1},x_{1:T},\lambda)$$
2. 从模型假设来看：

   HMM的假设建立在观测独立假设上，默认无视了状态间的相关性；

   MEMM打破了观测独立假设，在给定Y_t的情况下，X_t与X_t-1是联通的（与HMM相比，箭头是反向的），这样使得更加合理，因为状态序列是有一定相关性的。

3. 从输入输出来看：

   HMM是根据观测变量X，来预测隐变量Y，建模$P(XY)$联合概率分布；

   MEMM箭头反向了，是给定序列X，来预测Y，建模$P(Y|X)$的条件概率分布。

问题3：CRF改进了MEMM的什么问题？

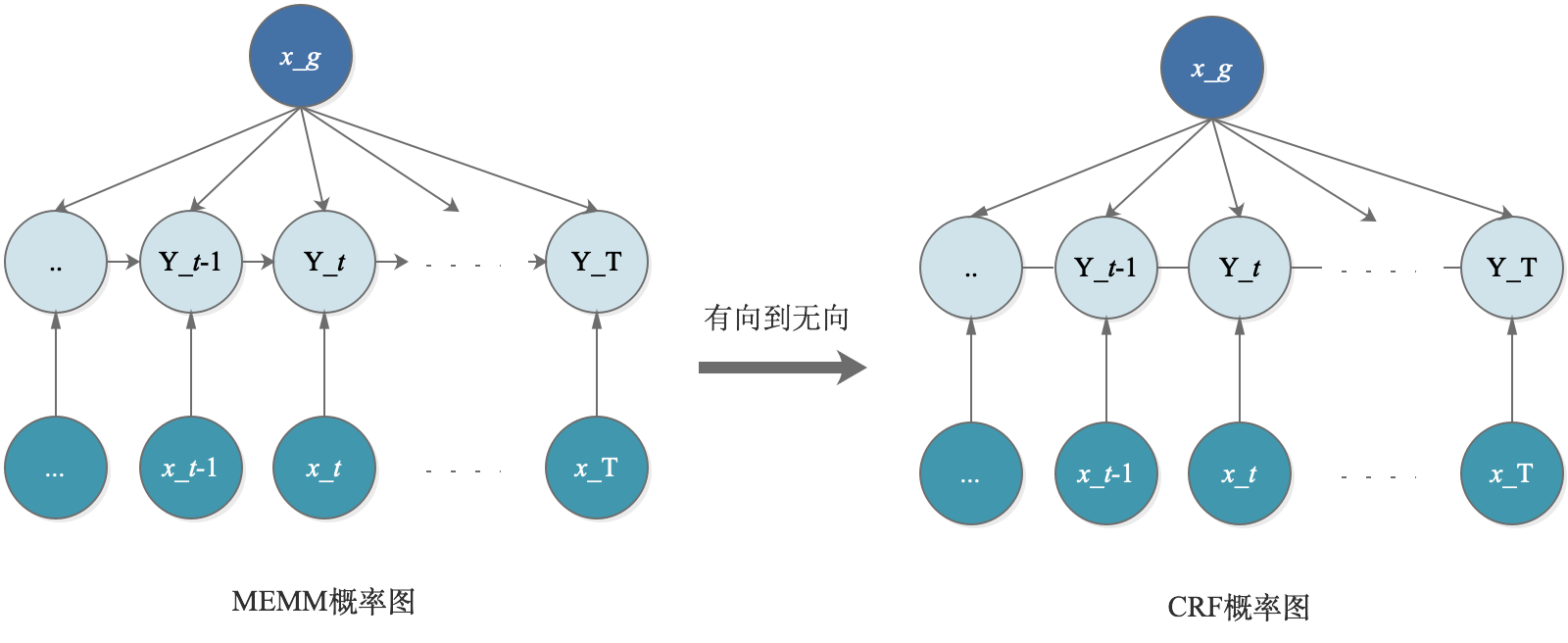
从直观上来看，CRF取消了待预测序列间的有向关系，从有向图变成了无向图，这样的好处在于：

改善了MEMM局部归一化所带来的label bias问题。

当概率图为有向图时，局部归一化是对序列的每一个step进行的；而当变成了无向图后，归一化是对于整个序列进行的，这样的预测对于序列是更加合理的，而不必受限于每一个step转移一定满足加和为1的约束。

问题4：介绍CRF？优化目标是？

介绍CRF：CRF是判别模型，即对于P(Y|X)进行建模，在给定序列X的情况下，来预测Y序列的值，是概率无向图模型。其满足马尔科夫性，且由于无向图的特性，在归一化操作上，是进行全局归一化的。模型中包含2种特征函数：节点特征函数，其仅与当前节点有关；局部特征函数，其仅与当前节点与上一节点有关（因为马尔科夫性）

优化目标：在给定N个训练数据中，训练优化特征函数对应的W矩阵：

$$\hat{W}=\mathop{argmax}_W \prod_{i=1}^N P(Y^{(i)}|X^{(i)})$$

问题5：CRF预测时，维特比算法的过程？

参考资料：https://www.zhihu.com/question/20136144

从S到A列的路径有三种可能：S-A1、S-A2、S-A3。我们不能武断的说S-A1、S-A2、S-A3中的哪一段必定是全局最短路径中的一部分，目前为止任何一段都有可能是全局最短路径的备选项。

我们继续往右看，到了B列。B列的B1、B2、B3逐个分析。遍历所有的下一步的可能状态，仅保留概率最大的，增量记录至当前候选路径中。

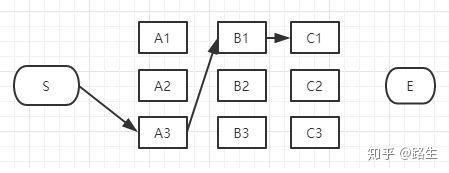
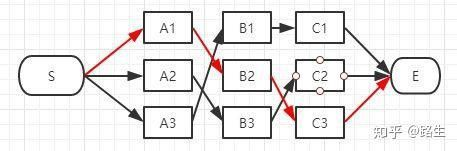
也就是说，在算法中，每到达一个step时，都会删除不符合最短路径要求的路径。

【Notes】

从最后一个step反向来看，确实是仅剩下了几条候选路径；

从第一个step正向单步筛选确定时，是把所有情况都遍历算了一遍的。