Transformer

本部分整理Transformer相关的的知识点内，2018年之后做NLP的如果说自己不会bert，恐怕是入行都是又困的，Transformer的Encoder正是Bert的基本组件。

参考资料：https://mp.weixin.qq.com/s/lPXlsXX0eS0EYBBNjqSBZA

另外一经典Blog：https://jalammar.github.io/illustrated-transformer/

上面经典blog的翻译：https://zhuanlan.zhihu.com/p/59629215

问题1：请你谈一谈Transformer？

Transformer是谷歌提出的完全用Attention进行特征提取的模型，模型是个典型的seq2seq模型，其中Encoder由若干个（多头self-attention和FFN）组成，Decoder由多头self-attention、多头Encoder-Decoder Attention、和FFN组成。为了能够训练序列的顺序信息，在Input中用sin-cos的方式对序列进行了编码。

对于Encoder是可以并行编码，在Decoder中通过mask的方式进行shift-right解码。

问题2：Transformer结构是什么样的？

模型总览：

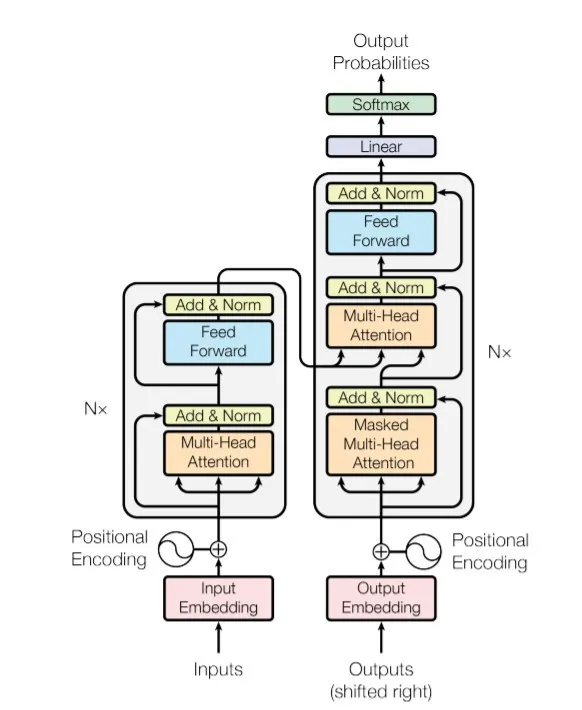
2.1 Encoder端

由 N(原论文中N=6)个相同的Block堆叠而成，其中每个Block又由两个子模块构成：

• 多头 self-attention 模块

• 前馈神经网络模块

注意：

1. 第一个Block(最底下的那个)接收的输入是输入序列的 embedding(embedding 可以通过 word2vec 预训练得来)；

2. 其余Block接收的是其前一个Block的输出；

3. 最后一个Block的输出作为整个 Encoder 端的输出。

2.2 Decoder端

由 N(原论文中N=6)个相同的Block堆叠而成，其中每个大模块则由三个子模块构成：

• 多头 self-attention 模块

  • Q, K, V都是相同的

    $$Attention(Q,K,V)=Softmax\bigg(\frac{QK^T}{\sqrt{d_k} }\bigg) \cdot V$$
• 多头 Encoder-Decoder attention 交互模块

  • Q是self-attetion的输出

  • K，V是来自于Encoder的输出

• 前馈神经网络模块

注意：

1. 第一个Block(最底下的那个)训练时和测试时的接收的输入是不一样的：

   • 训练时：接收的输入一次送入整个Embedding，每个step通过Mask掉Self-Attention的方式实现shifted right；特别地，当step为1时，其输入为特殊的token：可能是目标序列开始的token，也可能源序列结束的token，也可能是其他（视其他任务而定）

   • 测试时：先生成第1个step的位置的输出，第二次预测时，再将其加入输入序列，以此类推直至预测结束

2. 其余Block接收的是同样是其前一个Block的输出；

3. 最后一个模块的输出作为整个Decoder端的输出。

2.3 其他细节部分

1. FFN模块

   $$FFN(x)=max(0,xW_1+b_1)W_2+b_2$$

   在标准Transformer中，是用relu激活的；在Bert中，是用gelu激活的；

2. add & Norm部分

   • Add 表示残差连接（详见：XX）

   • Norm 表示 LayerNorm（详见：XX）

   残差连接来源于论文Deep Residual Learning for Image Recognition[1]，LayerNorm 来源于论文Layer Normalization[2]。

   $$Output = LayerNorm(x+Sublayer(x))$$
3. Position Embedding

   使用不同频率的正弦和余弦函数，公式如下：

   $$\begin{align} PE_{(pos,2i)} &= sin \bigg( \frac{pos}{10000^{2i/dim}} \bigg) \\ \\ PE_{(pos,2i+1)} &= cos \bigg( \frac{pos}{10000^{2i/dim}} \bigg) \end{align}$$

   注意：

   • Transformer的Position Embedding不是学习来的，是直接计算来的；

   • Bert中的Position Embedding可是通过预训练过程中训练得到的。

问题3：Self-Attention什么作用？为什么强大？

self-attention，是一种通过自身和自身相关联的 attention 机制，从而得到一个更好的 representation 来表达自身，self-attention 可以看成一般 attention 的一种特殊情况，是Soft-Attention分类下的。

在 self-attention 中，序列中的每个单词(token)和该序列中其余单词(token)进行 attention 计算。self-attention 的特点在于：

无视词(token)之间的距离直接计算依赖关系，从而能够学习到序列的内部结构，且实现起来也比较简单。

子问题3.1：Self-Attention与RNN相比捕捉远端依赖？

• RNN 或者 LSTM：需要依次序序列计算，对于远距离的相互依赖的特征，要经过若干时间步步骤的信息累积才能将两者联系起来，而距离越远，有效捕获的可能性越小；

• Self Attention：会更容易捕获句子中长距离的相互依赖的特征，且计算简单，不用依靠时间步骤的累积，直接建立起两者间的联系

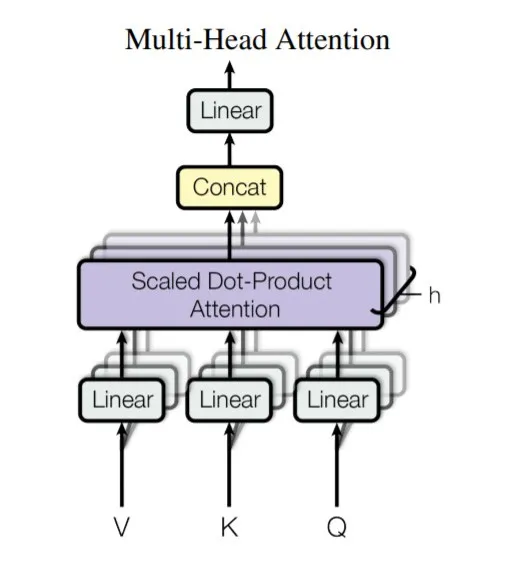
问题4：为什么使用多头？使用多头Attention的作用？

Transformer网络由多个层组成，每个层都由多头注意力机制和前馈网络构成。由于在全局进行注意力机制的计算，忽略了序列中最重要的位置信息。Transformer为输入添加了位置编码（Positional Encoding），使用正弦函数完成，为每个部分的位置生成位置向量，不需要学习，用于帮助网络学习其位置信息。

问题5：Self-Attention中为什么要做Scaled？作用是什么？

参考材料：

https://www.zhihu.com/question/339723385/answer/811341890

https://zhuanlan.zhihu.com/p/79585726

在数量级比较大的时候，softmax会把概率全部分配给了最大值，趋近于得到一个One-Hot的向量，进而导致SoftMax的梯度消失，造成更新困难。证明如下：

假设固定输入$X\in R^n$不变，变化参数$\beta$，假设输入$X$中有唯一的最大值$x_k$，则有：

$$\begin{align} \mathop{lim}\limits_{\beta \to + \infty}\sigma_\beta(X)_i &= \mathop{lim}\limits_{\beta \to + \infty} \frac{exp(\beta x_i)}{\sum_{j=1}^n exp(\beta x_j)} \\ \\ &= \mathop{lim}\limits_{\beta \to + \infty} \frac{1}{1 + \sum_{j=1,j \ne i}^n exp\Big( \beta (x_j - x_i)\Big)} \end{align}$$

不妨设$g(X,\beta,i)=\sum^n_{j=1,j \ne i} exp \Big(\beta (x_j - x_i)\Big)$，可以分类讨论一下：

1. 当$i=k$，则$\forall j \ne i, x_j-x_i<0$，此时：

   $$\mathop{lim}\limits_{\beta \to + \infty}g(X,\beta,i)=0$$
2. 当$i\ne k$，则$\exists j \ne i, x_j-x_i>0$，此时：

   $$\mathop{lim}\limits_{\beta \to + \infty}g(X,\beta,i)=+\infty$$

因此，结合上面的推导，可以得到：

$$\mathop{lim}\limits_{\beta \to + \infty} \sigma_\beta(X)_i= \left\{\begin{align}1,i=k\\\\0,i\ne k\end{align}\right.$$

即，当$\beta$取无穷大时，非标准softmax的输出收敛到一个one-hot向量，其中最大输入对应的输出值是1，其他输出是0。

然后我们看，这样趋向于输出One-Hot对于梯度的影响。

不妨简记softmax函数为$g(\cdot)$，softmax得到的分布向量$\hat y=g(X)$。对于输入$X$的梯度为：

$$\frac{\partial g(X)}{\partial X}=diag(\hat y)-\hat y \hat y^T$$

把这个矩阵展开：

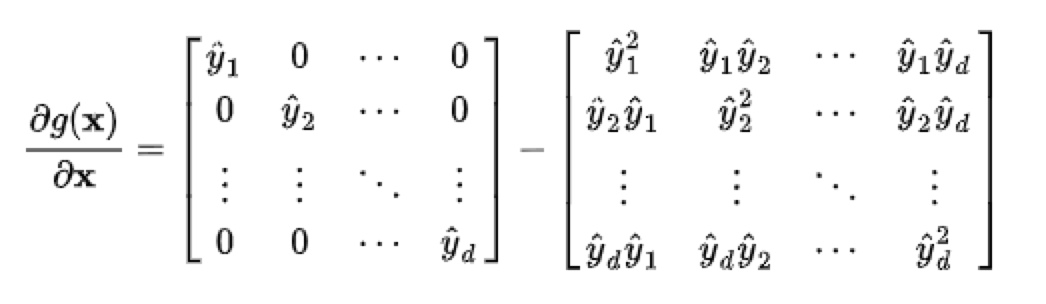
根据前面，当X元素都比较大的时候，会产生一个近似One-Hot的向量，那么此时，上面的矩阵就近似为0了。

下面再看维度与点积之间得到关系，为什么用维度的根号来缩放？

假设向量$q$和$k$的各个分量是互相独立的随机变量，均值是0，方差是1，那么点积$q \cdot k$的均值是0，方差是$d_k$。下面是推导：

对于$\forall i=1,...,d_k$，$q_i$和$k_i$都是随机变量，为了方便书写，不妨记$X=q_i$，$Y=k_i$。这样有：$D(X)=D(Y)=1$，$E(X)=E(Y)=0$

那么，则有：

1. $E(XY)=E(X)E(Y)=0\times 0 =0$

$$\begin{align} D(XY) &= E(X^2\cdot Y^2)-[E(XY)]^2 \\ &= E(X^2)E(Y^2) - [E(X)E(Y)]^2 \\ &= E(X^2 -[E(X)]^2)E(Y^2 -[E(Y)]^2)-[E(X)E(Y)]^2 \\ &= D(X)D(Y)-[E(X)E(Y)]^2 \\ &= 1 \times 1 - (0 \times 0)^2 \\ &= 1 \end{align}$$

这样$\forall i=1,...,d_k$，$q_i \cdot k_i$的均值是0，方差是1。又由期望和方差的性质，对相互独立的分量$Z_i$，有：

$$E(\sum_i Z_i)=\sum_i E(Z_i) \\ \\ D(\sum_i Z_i)=\sum_i D(Z_i) \\$$

所以有$q \cdot k$的均值是$E(q \cdot k)=0$，方差$D(q \cdot k)=d_k$。方差越大也就说明，点积的数量级越大（以越大的概率取大值）。那么一个自然的做法就是把方差稳定到1，做法是将点积除以$\sqrt{d_k}$ ，这样有：

$$D(\frac{q \cdot k}{\sqrt{d_k}})=\frac{d_k}{(\sqrt{d_k})^2}=1$$

将方差控制为1，也就有效地控制了前面提到的梯度消失的问题。

问题6：Transformer与seq2seq比优势在与什么？

seq2seq 最大的问题在于：将 Encoder 端的所有信息压缩到一个固定长度的向量中，并将其作为 Decoder 端首个隐藏状态的输入，来预测 Decoder 端第一个单词(token)的隐藏状态。

• 在输入序列比较长的时候，这样做显然会损失 Encoder 端的很多信息；

• 而且这样一股脑的把该固定向量送入 Decoder 端，Decoder 端不能够关注到其想要关注的信息。

问题7：Transformer 相比于 RNN/LSTM，有什么优势？为什么？

1. RNN系列的模型并行计算能力比较差

   • 因为RNN的建模过程是当前Cell依赖于上一个Cell的输出，必须序列建模才能抽取到信息特征；

   • 而Transformer的Encoder的Self-Attention是可以无视序列的step顺序关系，建模整个query的依赖关系，所以是可以并行执行的

2. Transformer特征提取能力从在一些主流任务的实验表现优于RNN系列

   • 因为Transformer一定程度上，通过self-attention的方式，摒弃了RNN系列step-by-step的建模方式，可以通过直接计算Attention的weight的方式来建模，从一定程度上能够强化更长远依赖的建模能力；但这并不表明可以无脑Transformer，遇到任务还是需要具体问题具体分析。