优化方法

参考资料：[1].深度学习中的优化算法、[2].一文看懂常用的梯度下降算法、[3].一个框架看懂优化算法之异同 SGD/AdaGrad/Adam、[4].SWATS算法剖析（自动切换adam与sgd）

深度学习优化算法经历了 SGD -> SGDM -> NAG ->AdaGrad -> AdaDelta -> Adam -> Nadam 这样的发展历程。

这块知识我是属于几乎完全空白的状态，这里按照优化算法的发展历程，分别梳理个优化算法（改进之处以及仍存在的缺点问题）。

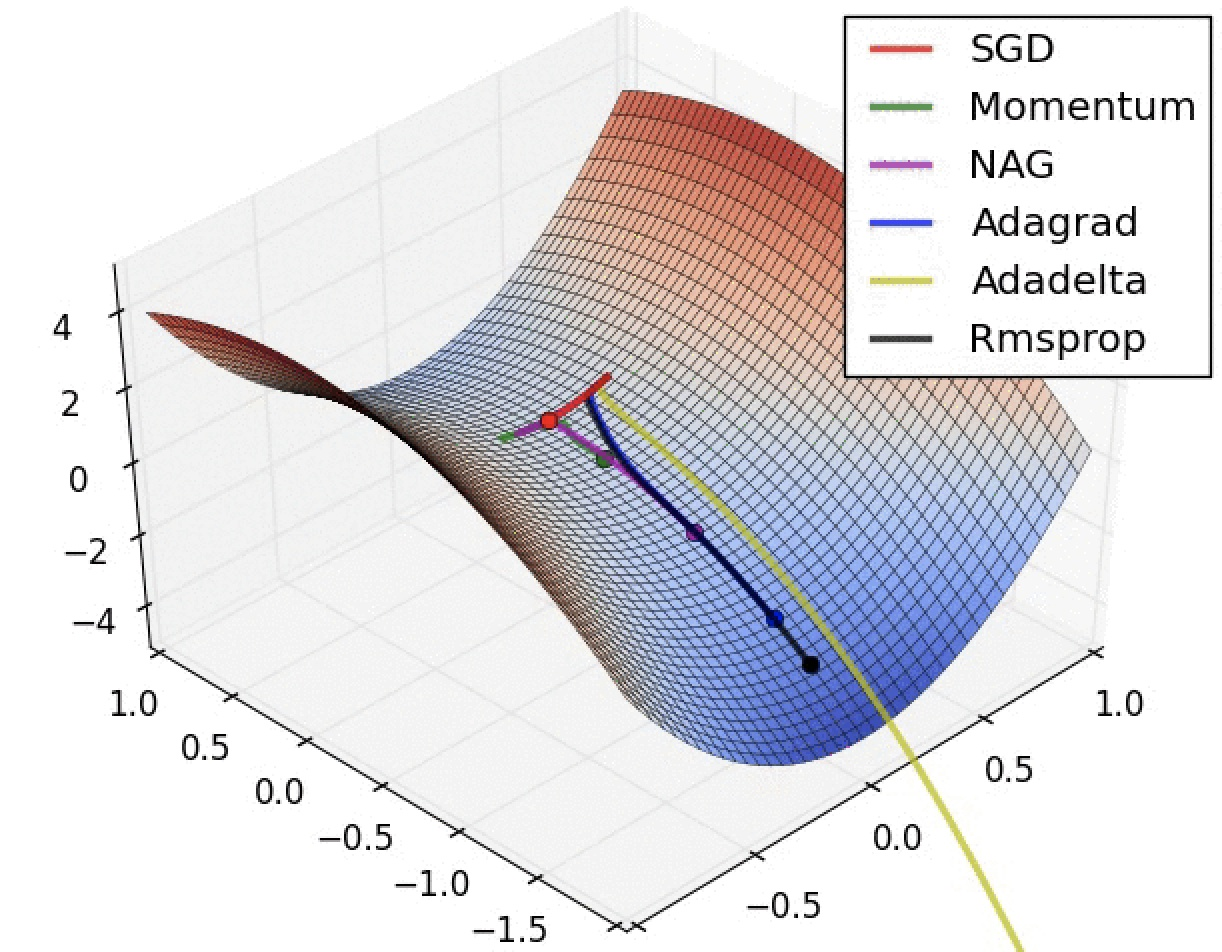
问题1：什么是指数加权移动平均数？

Exponentially weighted moving averages，这个概念在后面几个优化算法中都会用到。

针对序列数据，比如t时刻的观测值为x(t)，那么评估t时刻的移动平均值为：

$$v(t) \gets \beta \cdot v(t-1)+(1-\beta) \cdot x(t)$$

从0时刻，将式子进行展开：

$$\begin{align} v(0) &= 0 \\ v(1) &= \beta \cdot v(0)+(1-\beta) \cdot x(1) \\ v(2) &= \beta \cdot v(1)+(1-\beta) \cdot x(2) =\beta(1-\beta)\cdot x(1) + (1-\beta)\cdot x(2) \\ v(t) &= \sum^{t}_{i=1} \beta^{t-i}(1-\beta)\cdot x(i) \end{align}$$

也就是说：距离当前时刻较近的数据会对当前值影响较大，这样计算的好处是平均数会比较平稳。

问题2：SGD算法？

SGD也是随机梯度下降算法，是最简单的一种优化算法。

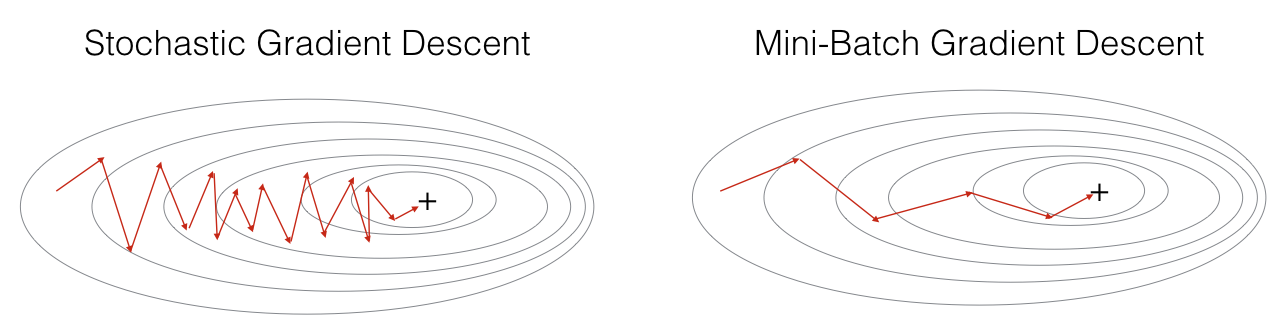
现在的SGD一般都指mini-batch gradient descent。

【问题】Batch/Mini-batch/stochastic gradient descent的区别？

• 【Batch gradient descent】 就是一次迭代训练所有样本；

• 【Stochastic gradient descent】每次只训练一个样本去更新参数；

• 【mini-batch gradient descent】每次用batch_size个样本来更新参数。

随机梯度下降法完全依赖于当前Batch，学习率可以理解为：允许当前Batch的梯度多大程度影响参数更新。

缺点主要在于：

• 合适的Learning Rate。（下降速度慢）

  SGD对所有的参数更新都使用同样的learning rate。但是，有时我们想：对于不经常出现的特征，更新快一些；对于常出现的特征，更新慢一些，这时候SGD就不太能满足要求了。

• SGD容易收敛到局部最优，并且在某些情况下可能被困在鞍点。

问题3：Momentum、Nesterov Acceleration改进了SGD算法的什么？

3.1 SGD with Momentum

冲量梯度下降算法是Boris Polyak在1964年提出的，其基于这样一个物理事实：将一个小球从山顶滚下，其初始速率很慢，但在加速度作用下速率很快增加，并最终由于阻力的存在达到一个稳定速率。

【第1种表述方式】

参数更新时不仅考虑当前梯度值，而且加上了一个积累项（冲量），但多了一个超参，一般取接近1的值如0.9。相比原始梯度下降算法，冲量梯度下降算法有助于加速收敛。当梯度与冲量方向一致时，冲量项会增加，而相反时，冲量项减少，因此冲量梯度下降算法可以减少训练的震荡过程。

【第2种表述方式】

按照上述算法看可能并不是很直观，有时候冲量梯度下降算法可以写成下面的形式：

$$\begin{align} 速度更新&:v \gets \alpha \cdot v + (1-\alpha)\cdot g\\ 参数更新&:\theta \gets \theta - \eta \cdot v \end{align}$$

此时我们就可以清楚地看到，所谓的冲量项其实只是梯度的指数加权移动平均值（问题1中阐述的）。

与SGD相比改进之处：

• 针对于SGD，改进了梯度的下降量，（因为引入了冲量概念，即梯度的指数加权移动平均值），因此而带来的好处是让SGD的下降更稳定。

3.2 SGD with Nesterov Acceleration

NAG算法是Yurii Nesterov在1983年提出的对冲量梯度下降算法（SGD with Momentum）的改进版本，其速度更快。其变化之处在于计算“超前梯度”更新冲量项。

Nesterov的改进（与Momentum相比）：就是让之前的动量直接影响当前的动量，表达形式：

$$\begin{align} 超前梯度计算&：g \gets \bigtriangledown _\theta \sum^{m}_{i} L(f(x^{(i)};(\theta-\alpha \cdot v)),y^{(i)})/m \\ 更新量计算&:v \gets \alpha \cdot v + \eta \cdot g \\ 参数更新&:\theta \gets \theta - v \end{align}$$

Momentum算法中，在时刻t的下降方向是由累计的动量决定的；

NAG算法中，根据累计的动量再计算一步未来位置上的梯度，然后一起叠加到参数的更新量中。

与SGD with Momentum的改进之处：

• 能够一定程度解决困在局部最优的沟壑中。通俗的理解NAG就是：我们不能停留在当前位置去观察未来的方向，而要向前一步、多看一步、看远一些。

问题4：AdaGrad改进了什么？

AdaGrad是Duchi在2011年提出的一种学习速率自适应的梯度下降算法。

【提出AdaGrad算法的原因】

无论是SGD、Momentum、NAG，这都对梯度计算进行的优化，也就是使更新的梯度更加灵活；但是，人工设置固定的学习率是生硬的，在整个训练过程中是一直不变的，所以需要自适应调整学习率的算法。

【特点及意义】

特点在于：

• 前期梯度累计量较小时，能够放大梯度；

• 后期梯度累计量较大时，作为学习率的约束项是在学习率的分母位置，能够起到缩小梯度；

意义在于：

• 对于经常更新的参数：我们已经积累了大量关于它的知识，不希望被单个样本影响太大，希望学习速率慢一些；

• 对于偶尔更新的参数：我们了解的信息太少，希望能从每个偶然出现的样本身上多学一些，即学习速率大一些。

【缺点】

• 随着训练的进程进展，会导致累加和太大而使得更新量趋近于0，使训练提前结束，这是我们所不愿意看到的。

• 仍然依赖于全局学习率。

问题5：AdaDelta解决了什么问题？

AdaDelta是对于AdaGrad的优化。是为了解决不断累积的梯度平方值过大的问题：不累积全部历史梯度，而只关注过去一段时间窗口的下降梯度。

AdaDelta原文：https://arxiv.org/pdf/1212.5701.pdf

其中：

$$\begin{align} RMS[\Delta x]_t &= \sqrt{E[\Delta x^2]_t+\epsilon}\\ RMS[g]_t &= \sqrt{E[g^2]_t+\epsilon} \end{align}$$

【特点】

• 这里不再是累加全部的历史项，而是使用移动加权平均的方式，可以解决掉AdaGrad累加过大的问题；

• 作者做了一定处理，经过近似牛顿迭代法之后，可以看出Adadelta已经不用依赖于全局学习率了。

问题6：RMSprop

RMSprop算法与AdaDelta对于AdaGrad的优化思路很想，但是唯一的区别在于：RMSprop并没有摆脱对于全局学习率的依赖。

改进思路：仍然是与AdaDelta一样，用一段时间内的累计量来替代全部历史的累积量（还是指数移动加权平均数的套路）

问题7：Adam算法原理？Nadam改进了什么？

7.1 Adam算法原理？

SGD-M在SGD基础上增加了一阶动量，AdaGrad和AdaDelta在SGD基础上增加了二阶动量。把一阶动量和二阶动量都用起来，就是Adam了——Adaptive + Momentum。

m用于保存一阶动量，v用于保存二阶动量：

$$\begin{align} m_t &= \beta_1 m_{t-1}+(1-\beta_1) \cdot g_t \\ v_t &= \beta_2 v_{t-1}+(1-\beta_2) \cdot g_t^2 \end{align}$$

PS：当mt和vt初始化为0的时候，在初期，这个值是趋于0的，这是我们不想看到的。所以，需要做一个误差修正：

$$\begin{align} \hat m_t = \frac{m_t}{1-\beta_1^t}\\ \hat n_t = \frac{n_t}{1-\beta_2^t}\\ \end{align}$$

可以看出，当迭代次数很小的时候，可以对mt和nt起到一个放大作用；而随着迭代的次数增加，分母几乎趋近于1，也就不用进行修正了。

梯度更新规则：

$$\theta_{t+1}=\theta_t-\frac{\hat m_t}{\sqrt{\hat v_t +\epsilon}}*\eta$$

7.2 Nadam与adam的区别？

Adam是集Momentum和AdaGrad于一身的。但是没有Nesterov呀，所以，引入Nesterov的adam就是Nadam。

问题8：Adam存在什么问题？

参考资料：https://zhuanlan.zhihu.com/p/32262540

主要存在二个比较大的问题：

• 可能不收敛

• 可能错过全局最优解

8.1 不收敛问题的根源

回忆一下上文提到的各大优化算法的学习率：

SGD与AdaGrad会使得学习率不断递减，最终收敛到0，模型也得以收敛：

• SGD没有用到二阶动量，因此学习率是恒定的（实际使用过程中会采用学习率衰减策略，因此学习率递减）

• AdaGrad的二阶动量不断累积，单调递增，因此学习率是单调递减的。

AdaDelta和Adam则会有学习率的震荡：

二阶动量是固定时间窗口内的累积，随着时间窗口的变化，遇到的数据可能发生巨变，使得窗口累积量时大时小，不是单调变化。这就可能在训练后期引起学习率的震荡，导致模型无法收敛。

8.2 错过全局最优解

主要是因为：自适应学习率算法可能会对前期出现的特征过拟合，后期才出现的特征很难纠正前期的拟合效果。

吐槽Adam最狠的 The Marginal Value of Adaptive Gradient Methods in Machine Learning 。

文中说到，同样的一个优化问题，不同的优化算法可能会找到不同的答案，但自适应学习率的算法往往找到非常差的答案。他们通过一个特定的数据例子说明，自适应学习率算法可能会对前期出现的特征过拟合，后期才出现的特征很难纠正前期的拟合效果。

Improving Generalization Performance by Switching from Adam to SGD，进行了实验验证。

他们CIFAR-10数据集上进行测试，Adam的收敛速度比SGD要快，但最终收敛的结果并没有SGD好。他们进一步实验发现，主要是后期Adam的学习率太低，影响了有效的收敛。他们试着对Adam的学习率的下界进行控制，发现效果好了很多。

问题9：Adam+SGD结合策略？SWATS算法

参见：https://zhuanlan.zhihu.com/p/32406552

SWATS的算法主要是：前期享受Adam的快速收敛，后期转向SGD获得更好的训练结果。

（有待进一步研究后整理补充）