Word2Vec

问题1：图解Word2Vec模型

整理摘自：https://www.jianshu.com/p/a92475dfb99a

首先，用Skip-Gram模型进行详细展开，然后，在补充上CBOW在Skip-Gram上具体操作上的区别之处。

1.1.生成训练数据

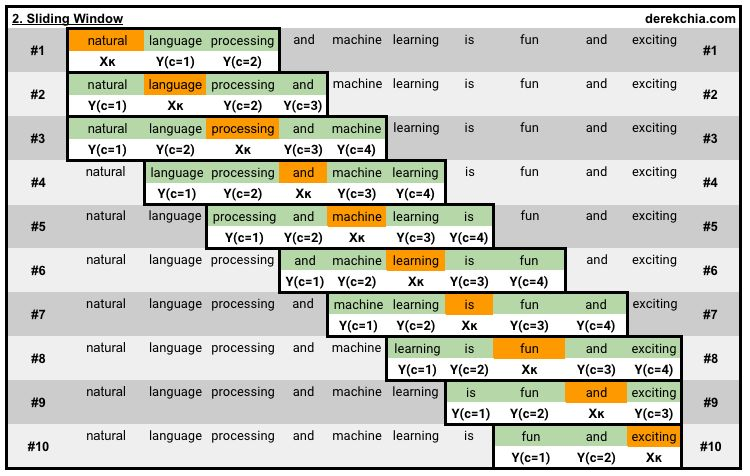
对于一句话，用window_size大小为2的滑窗进行切分句子（目标单词的前2个词+后2个词）。

例如：“natural language processing and machine learning is fun and exciting”。一个有有10个单词的一句话，其中有9个不重复的单词，用滑动窗口可以生成10组训练数据。

1.2.模型训练

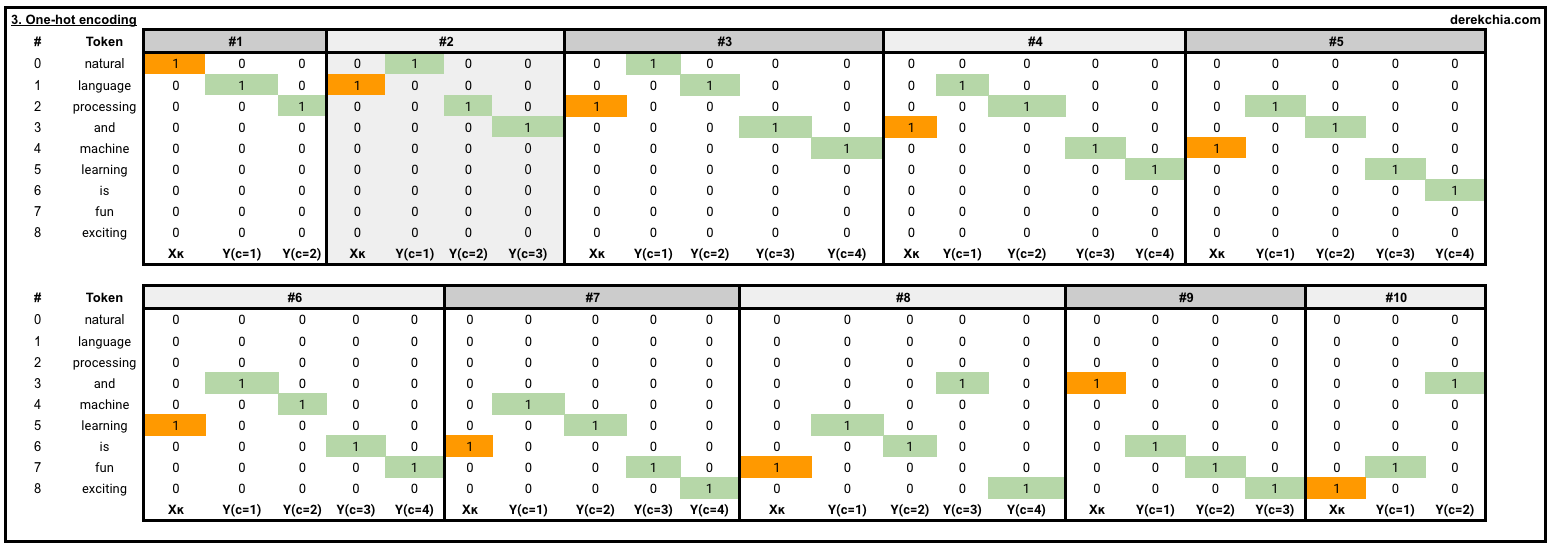
这样对于每一个词，都可以表示成1个9维的One-Hot向量。Word2Vec2模型有两个权重矩阵(w1和w2)，为了展示，我们把值初始化到形状分别为(9x10)和(10x9)的矩阵。

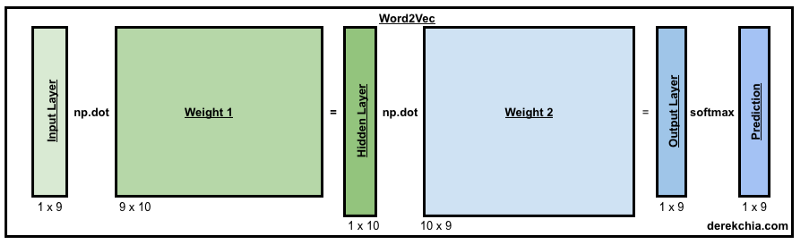
模型训练总共分为4个步骤：

  1. 前向计算

  2. 计算误差（EI）

  3. 计算Weight的修改量

  4. 修改Weight的值

1.2.1 Forward-process

以第一窗口（#1）中作为训练样本来展示计算过程：

其中目标词是“natural”，上下文单词是“language”和“processing”。

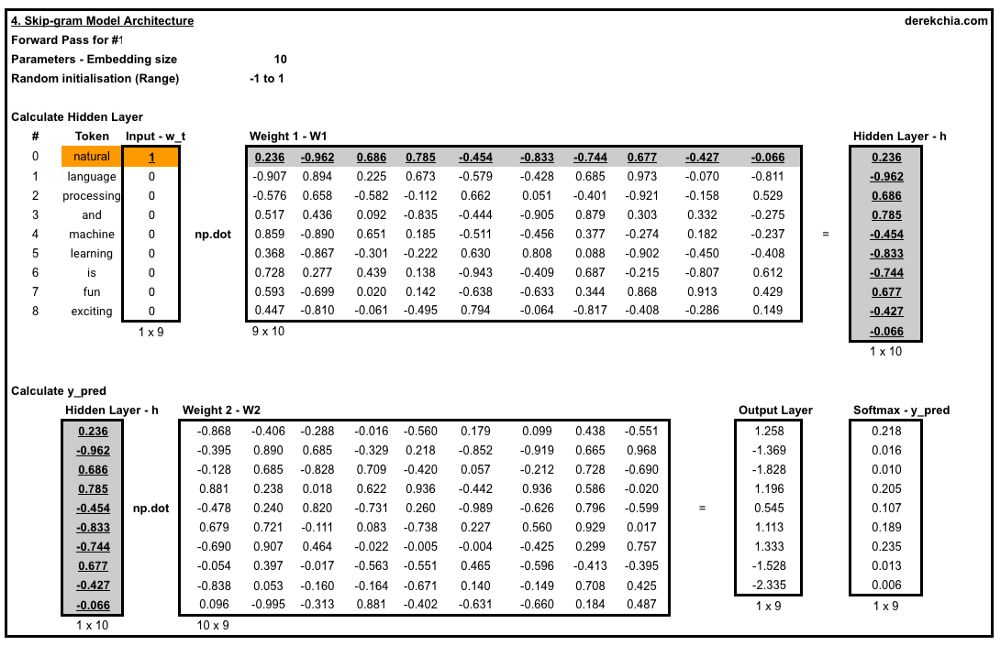
1.2.2 计算误差

注意，这里Skip-gram是用1个词来预测上下文的，所以在EI计算中，是对上下文词全都计算diff，然后进行加和，作为总的EI。

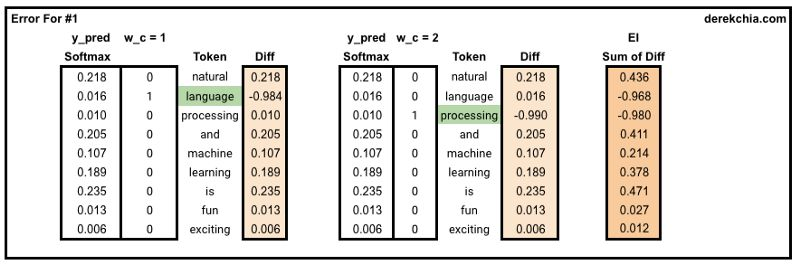
1.2.3 计算Weight1和Weight2的修改量

对于Weight2的修改量：用Hidden Layer和EI进行外积运算，得到10*9维的修改量矩阵；

对于Weight1的修改量：首先，将EI（转置）与Weight2进行相乘，得到Hidden Layer的Loss值；然后，用Input与Hidden Layer的Loss值进行外积运算，得到9*10维的修改量矩阵；

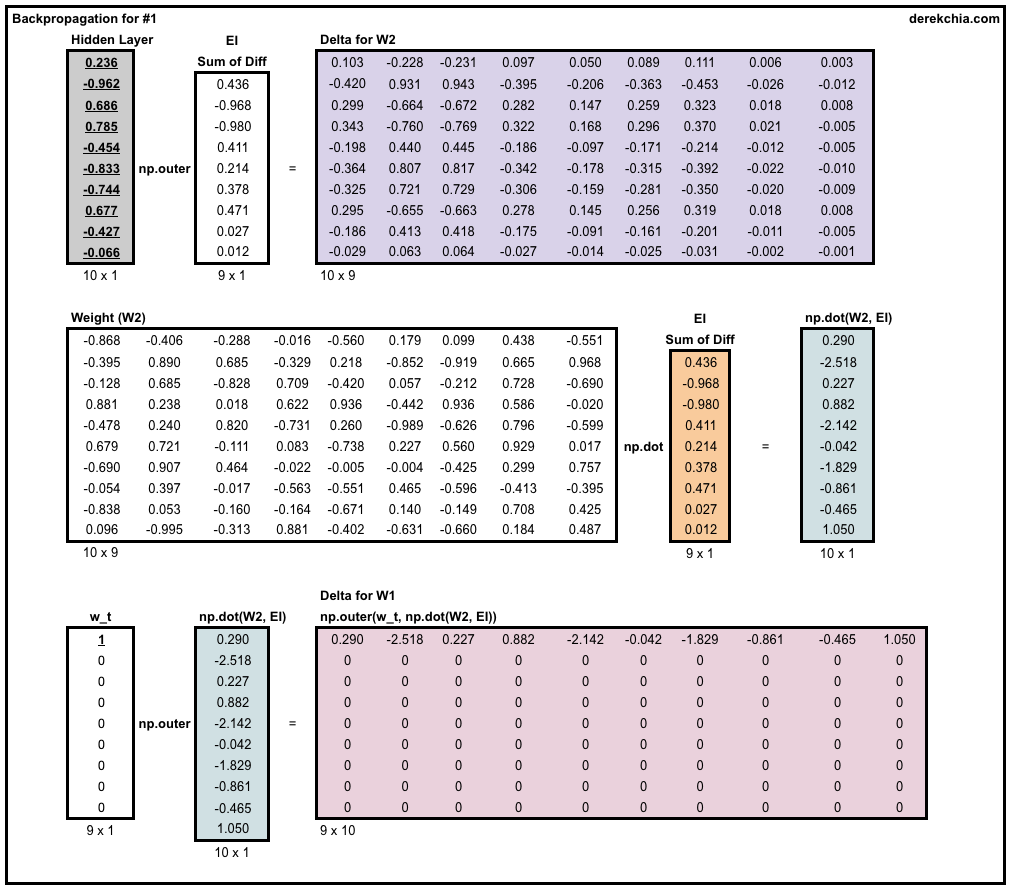
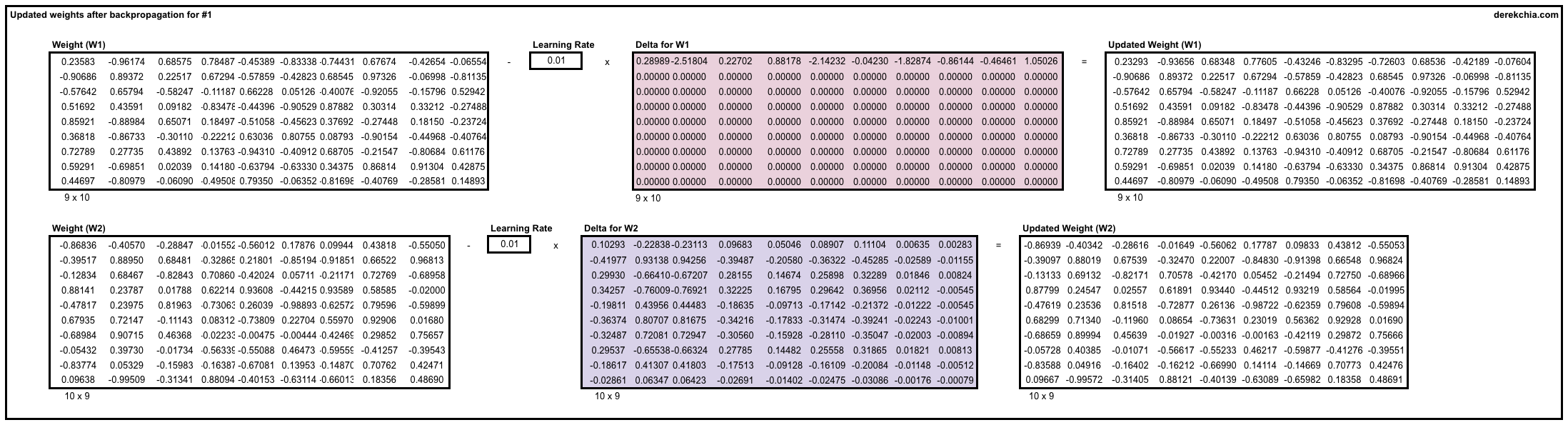
1.2.4 修改Weight1与Weight2

这里就将修改量与学习率进行相乘，从Weight中减下去就OK咯！

1.3. CBOW的区别之处

CBOW模型中，仍然是两个权重矩阵，Weight1和Weight2。主要区别就存在于对于Weight1权重矩阵这里。

1.3.1 Forward-Process

由于CBOW中是当前词的上下文来预测当前词，所以，就是用Weight1分别与当前词的所有上下文词进行相乘后，取平均，即为：

h=1CW⋅(∑i=1Cxi)h=\frac{1}{C} W\cdot(\sum^{C}_{i=1}x_i)

1.3.2 Backward-Process

  • 在计算误差时：softMax之后的结果只与预测词进行计算，得到EI（diff）。

  • 在计算Weight1的修正量时：依然是计算所有的上下文词与Hidden Layer的Loss外积，并乘以1/C，得到Weight1的修正量，这里就不详细列出计算公式了。

1.4.最终训练得到的词向量

最终，取Weight1的每一行，作为每一个词的词嵌入（一般称：Weight1为Input Embedding；Weight2为Output Embedding）。

问题2：Word2Vec中2种预测方式的区别？

先上图再说：

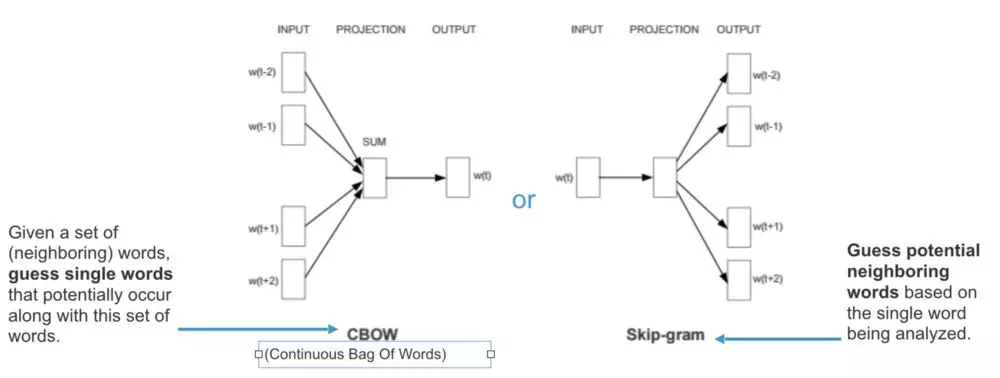
Word2Vec模型：是基于分布假说，其认为每个单词的上下文都在其附近的单词中。通过查看它的相邻单词我们可以尝试对目标单词进行预测。

二者在模型预测上形式的区别：

Continuous Bag-of-Words(CBOW)：尝试从相邻单词（上下文单词）猜测输出（目标单词）；

Skip-gram(SG)：从目标单词猜测上下文单词。

二者在模型效果上的区别：

CBOW：比skip-gram训练快几倍，对出现频率高的单词的准确度稍微更好一些

Skip-gram：能够很好地处理少量的训练数据，而且能够很好地表示不常见的单词或短语

问题3：为什么skip-gram能够很好表示不常见的单词？

由于Skip-gram学习用给定单词来预测上下文单词，所以万一两个单词（一个出现频率较低，另一个出现频率较高）放在一起，那么当最小化loss值时，两个单词将进行有相同的处理，因为每个单词都将被当作目标单词和上下文单词。与CBOW相比，不常见的单词将只是用于预测目标单词的上下文单词集合的一部分。

上面说的可能比较干巴巴的，下面用一个比较生动的例子进行进一步的解释：

CBOW是根据上下文来预测当前词。在CBOW中，先从反向思维来看：

比如这样一个句子yesterday was really a [...] day，中间可能是good也可能是nice，比较生僻的词是delightful。当CBOW去预测中间的词的时候，它只会考虑模型最有可能出现的结果，比如good和nice，生僻词delightful就被忽略了。

再从正向思维来看：

对于[...] was really a delightful day这样的句子，每个词在进入模型后，都相当于进行了均值处理，delightful本身因为生僻，出现得少，所以在进行加权平均后，也容易被忽视。

而Skip-Gram是根据一个词预测它的上下文。也就是用一个词预测多个词，每个词都会被单独得训练，较少受其他高频的干扰。所以对于生僻词Skip-Gram的word2vec更占优。

问题4：为什么CBOW训练速度比Skip-gram训练速度快？

CBOW预测行为的次数跟整个文本的词数几乎是相等的，因为是对上下文词的向量进行进行了加和平均正向/反向传播的，复杂度大概是O(V);

Skip-gram进行预测的次数是要多于CBOW的：因为每个词在作为中心词时，都要使用周围词进行预测一次，即上下文词都要对正向传播结果进行运算得到diff，再加和得到EI。这样相当于比CBOW的方法多进行了K次（假设K为窗口大小），因此时间的复杂度为O(KV)，训练时间要比CBOW要长。

问题5：负采样解决什么问题？如何优化的？

【解决的问题】：解决训练中更新维护超级庞大的权重矩阵太过缓慢的问题，以提高训练速度。

下面将详细展开NS（Negative Sampling）是如何优化的。

参考自：https://zhuanlan.zhihu.com/p/39684349

5.1 总括

负采样（negative sampling）是用来提高训练速度并且改善所得到词向量的质量的一种方法。不同于原本每个训练样本更新所有的权重，负采样每次让一个训练样本仅仅更新一小部分的权重，这样就会降低梯度下降过程中的计算量。

5.2 positive/negative sample

当我们用训练样本 ( input word: "fox"，output word: "quick") 来训练我们的神经网络时，“ fox”和“quick”都是经过one-hot编码的。如果我们的vocabulary大小为10000时，在输出层，我们期望对应“quick”单词的那个神经元结点输出1，其余9999个都应该输出0。

在这里，这9999个我们期望输出为0的神经元结点所对应的单词我们称为“negative” word。

而那1个我们期望输出为1的神经元结点所对应的单词我们称为“positive” word。

当使用负采样时，我们将随机更新1+N个词对应的权重：

  • 1即为：1个Positive Word

  • N即为：N个Negative Words

在论文中，作者指出指出对于小规模数据集，选择5-20个negative words会比较好，对于大规模数据集可以仅选择2-5个negative words。

假设：隐层-输出层拥有300 x 10000的权重矩阵。如果使用了负采样的方法我们仅仅去更新1个Positive+5个Negative words对应的权重，对于3百万的权重来说，相当于只计算300*6=1800个权重（占总权重的0.06%），这样计算效率就大幅度提高。

5.3 如何选择Negative words

我们使用“一元模型分布（unigram distribution）”来选择“negative words”。

一个单词被选作negative sample的概率跟它出现的频次有关：出现频次越高的单词越容易被选作negative sample。

一个单词被选为Negative Sample的概率公式如下：

P(wi)=f(wi)34∑j=0n(f(wi)34)P(w_i)=\frac{f(w_i)^{\frac{3}{4}}}{\sum^{n}_{j=0}(f(w_i)^{\frac{3}{4}})}

其中，f(wi)为单词的在语料中出现频次。

公式中开3/4的根号完全是基于经验的，论文中提到这个公式的效果要比其它公式更加出色。

5.4 负采样的目标函数是什么？

（参见学习原论文的解读论文：）

问题6：层次化SoftMax是如何工作的？

【概括】层次化SoftMax的精华就是充分利用了Huffman树的性质，减少了SoftMax对整个词表进行全计算的恐怖计算量。

6.1 Huffman树

【特点】节点的权越小，其离树的根节点越远。

6.1.1 Huffman树的构建

以一个例子来给出构建Huffman树的步骤：

节点名

节点权重

A

8

D

1

E

4

F

1

R

5

T

3

整个步骤的伪代码可以表示成如下的形式：

do while 剩余节点>1:
    按照权值对所有节点进行排序;
    选择权值最小的2个节点，构造二叉树（左孩子权值<右孩子权值）;
    生成新的节点，节点权值为构造的二叉树叶子节点权重之和，加入节点列表中;

按照上述步骤，那么Huffman树可以构造成如下形式：

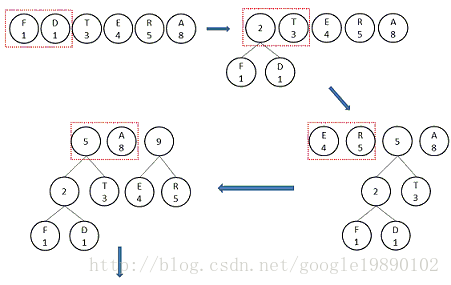
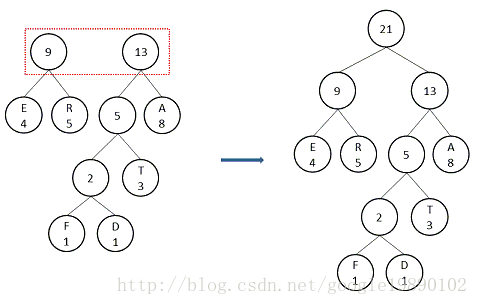
6.1.2 Huffman树的性质

  • 1.Huffman树不存在度为1的节点。

    因为每一步都是选择2个节点构造二叉树，所以，节点的度要么是0，即为叶子节点；要么就是2，即为非叶子节点

  • 2.Huffman树的节点总数可表示为：设叶子节点数为N，那么，非叶子节点数为N-1，总节点数为2N-1。

  • 3.Huffman数的不唯一。

    因为在构造的过程中，会产生存在权重相同的节点，在选择最小的2个节点来构造二叉树时，就会产生差异的。

6.2 Hierarchical Softmax

【解决的问题】优化SoftMax需要对语料库中每个词语（类）都计算一遍输出概率并进行归一化的问题，降低计算量。

在Word2Vec中，最后需要对输出进行计算SoftMax，如下：

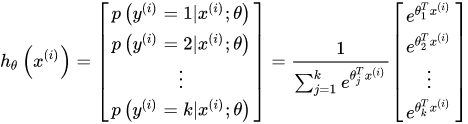
问题7：什么情况下更倾向于使用skip-gram？什么情况下更倾向于CBOW？

问题8：FastText与Word2Vec的区别？

（这个问题详见FastText知识章节）

上一页中文NER总结下一页Transformer

最后更新于

这有帮助吗？