特征工程

特征工程是在机器学习中做数据挖掘中非常重要的一个内容，能够决定算法的效果的：算法会有所影响，但与特征的好坏相比，影响就没有那么的明显了。

问题1：归一化

1.1 为什么数值型数据需要归一化？

答：这里就引用到一张非常经典的“椭圆梯度下降的等高线VS圆形梯度下降等高线”。

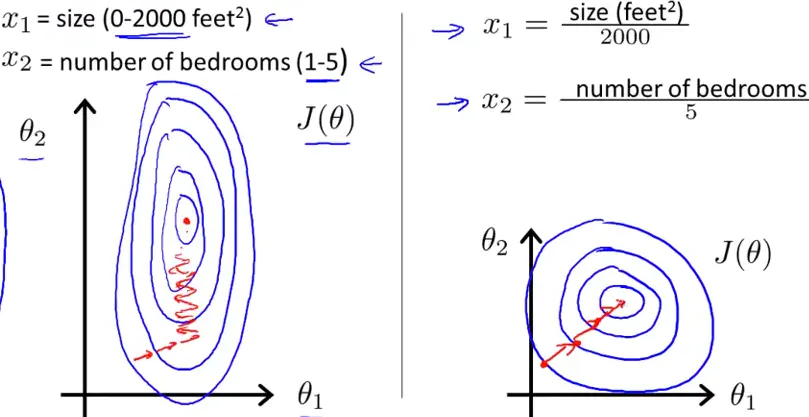
在未进行归一化时，不同维度上的下降速率不同，会导致在梯度下降时的抖动不稳定，不利于在较少的迭代中找到最优解（椭圆等高线）。

1.2 什么样的模型需要进行数值归一化？

需要归一化的模型：线性回归、逻辑回归、支持向量机、神经网络

不需要归一化的模型：决策树相关模型

【进一步】为什么决策树相关模型不需要归一化？

答：因为决策树是在某一特征维度的值域上进行选择分裂点，而选择分裂点的依据并不受到特征值是否有归一化的影响，因此不需要归一化。

问题2：类别编码

2.1 如何根据场景进行类别数据编码？

类别数据编码方式：有序号编码、独热编码。

序号编码即是直接将类别按照顺序依次编码；独热编码就是One-Hot转换成一个N维度向量。

【进一步】如何选择问题？

序号编码：这保留了类别之间的大小关系：高中低、大中小这样的潜在属性关系；

from sklearn.preprocessing import LabelEncoder
class_le = LabelEncoder()
y = class_le.fit_transform(df['classlabel'].values)

# 还原原值类别值
class_le.inverse_transform(y)

独热编码：类别之间并无直接的关系。

from sklearn.preprocessing import OneHotEncoder
ohe = OneHotEncoder(categorical_features=[0])
ohe.fit_transform(X).toarray()

【独热编码-推荐】

其实更推荐直接用pandas的get_dummies，直接获取字符串类型的哑特征。

# 需要进行转换的列
a = ['price', 'color', 'size']
# 转换成哑变量
pd.get_dummies(df[a])

PS：在使用Xgb时，超级稀疏的特征对于模型会有什么影响？Xgb是如何处理类别特征的？【在决策树专题中的Xgb会补充上】

问题3：特征选择

3.1 特征选择原则？

在构建特征工程时，例如构建了数十维的特征，那么如何在特征中进行选择？选择什么样的特征进行删除？【当然除了纯人工手动去过滤外】

• 缺失值过多的特征

  因为缺失值确实过多会导致无法从特征的分布中学习到数据的潜在规律

• 共线性特征

  当2个具有共线性时，会导致模型过多的学习到该共线性的分布。

  【如何分析共线性问题？】通过计算皮尔斯相关系数来进行计算，相关系数的绝对值大于阈值的，可判定为共线性很强的特征对。

• 低重要度特征

  【如何计算重要度？】这个问题其实属于树模型中的问题。在树模型中选择分裂点时，会对当前状态下选择信息增益最大的特征和分裂点进行分裂，因此，对于特征而言，特征的重要度即为：该特征带来的信息增益的总量（标准化后的，在集成模型下，那就是多棵树下的加和）

  【扩展】在DecisionTree、Xgb、lgb中计算特征重要度的API：https://www.jianshu.com/p/2110409fbc24

Will Koehrsen最近开源了一个特征选择神器。黄博士对其进行进行了翻译，并给出了使用范例。

3.2 Boruta特征选择算法？

Boruta算法同样也是一种特征重要度计算的算法，但是不同于上面对于特征在树模型中根据信息增益来计算得到的。

算法的github：https://github.com/scikit-learn-contrib/boruta_py

算法的主要思路为：

1. 创建阴影特征 (shadow feature) : 对每个真实特征R，随机打乱顺序，得到阴影特征矩阵S，拼接到真实特征后面，构成新的特征矩阵N = [R, S].

2. 用新的特征矩阵N作为输入，训练模型，能输出featureimportances的模型，如RandomForest， lightgbm，xgboost都可以，得到真实特征和阴影特征的feature importances；

3. 取阴影特征feature importance的最大值S_max，真实特征中feature importance大于S_max的，记录一次命中；

4. 用(3)中记录的真实特征累计命中，标记特征重要或不重要。原论文中用Bonferroni校正作显著性检验，boruta_py认为Bonferroni校正太过保守，默认增加了FDR校正，用two_step参数可以切换两种检验方法。

5. 删除不重要的特征，重复1-4，直到所有特征都被标记。

训练结束后，boruta_py 还可以输出特征ranking_，表示特征的重要性等级，在特征选择中也是一个很有用的指标。