激活函数

参考资料：[1]. GELU 激活函数、[2]. [Deep Learning] GELU (Gaussian Error Linerar Units) 、[3]. 从ReLU到GELU，一文概览神经网络的激活函数

问题1：激活函数的意义？

在没有激活函数的时候，网络的表达能力有限，无论多少层的网络结构都可以退化表示成一个单层的线性网络。

那么它的意义在于：

1. 模拟生物神经元特性，接受输入后通过一个阈值模拟神经元的激活和兴奋并产生输出。

2. 为神经网络引入非线性，增强神经网络的表达能力。

问题2：Sigmoid函数？

sigmoid 函数是一个 logistic 函数，意思就是说：不管输入是什么，得到的输出都在 0 到 1 之间。也就是说，你输入的每个神经元、节点或激活都会被缩放为一个介于 0 到 1 之间的值。

$$sigmoid(x)=\frac{1}{1+e^{-x}}$$

他的函数图像如下图：

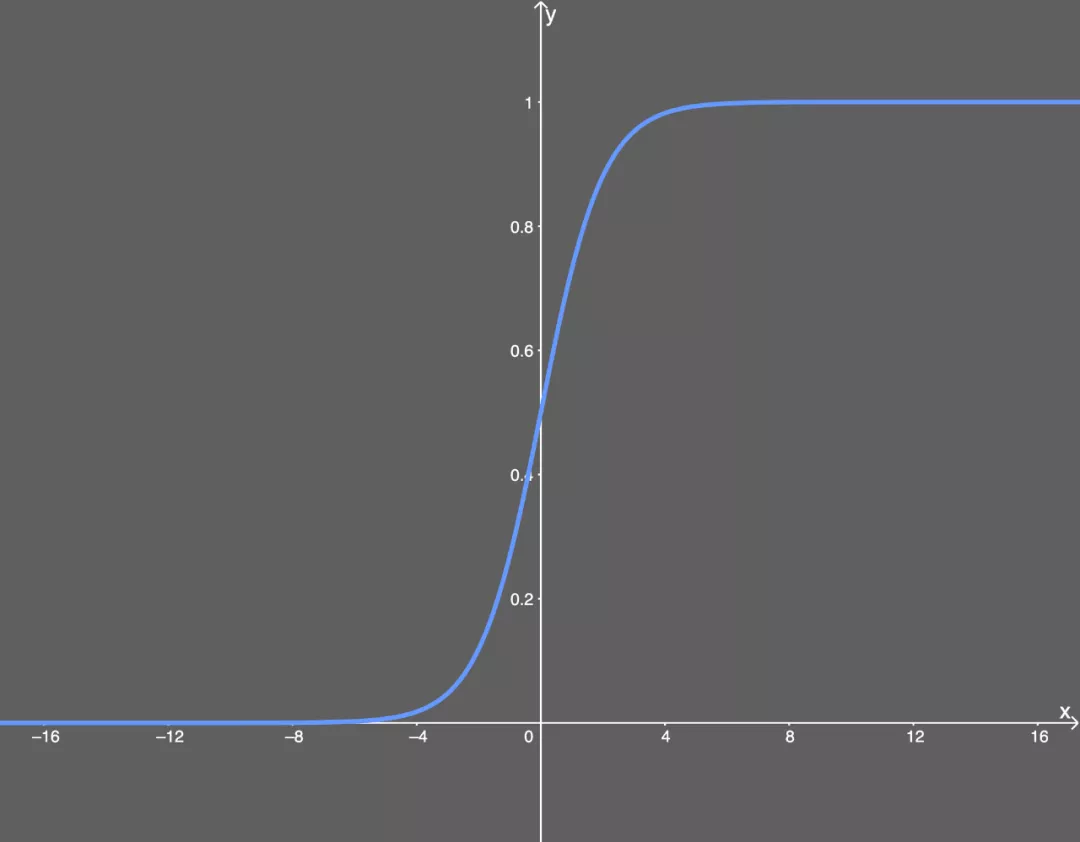
2.1 Sigmoid缺点

【梯度消失】Sigmiod问题出在了当x较大时，其导数近乎为0，那么在反向传播时，每一个参数的更新量都会去乘上这个近乎为0的值，也就几乎不会产生什么太多的变化，即为梯度消失。

因为其导数为：

$$\sigma'(x)=\sigma(x)(1-\sigma(x))=\frac{e^{-x}}{(e^{-x}+1)}$$

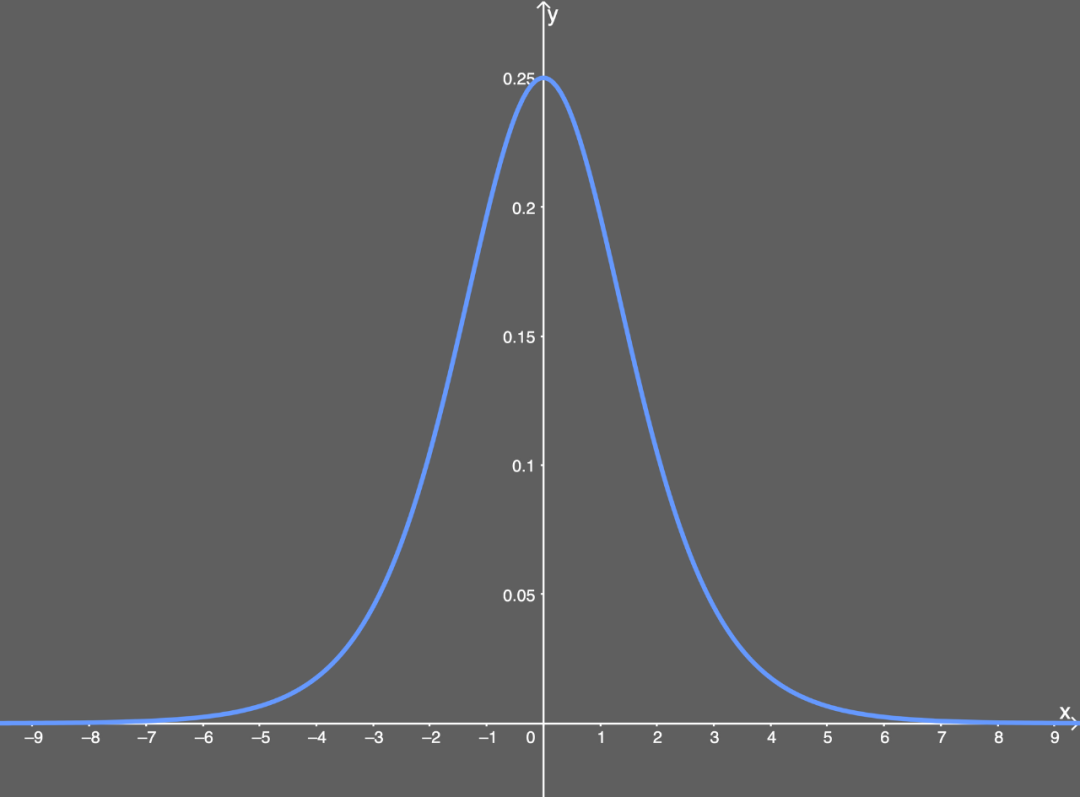
问题3：ReLU函数？

整流线性单元是解决梯度消失问题的方法，但是ReLU还是存在一定问题的。

ReLU的公式如下：

$$ReLU(0,x)=max(0,x)$$

其公式的含义为：

• 如果输入 x 小于 0，则令输出等于 0；

• 如果输入 x 大于 0，则令输出等于输入。

那这跟解决梯度消失有什么关系呢？

$$ReLU'(x)=\left\{\begin{align}0,x<0\\\\1,x\ge0\end{align}\right.$$

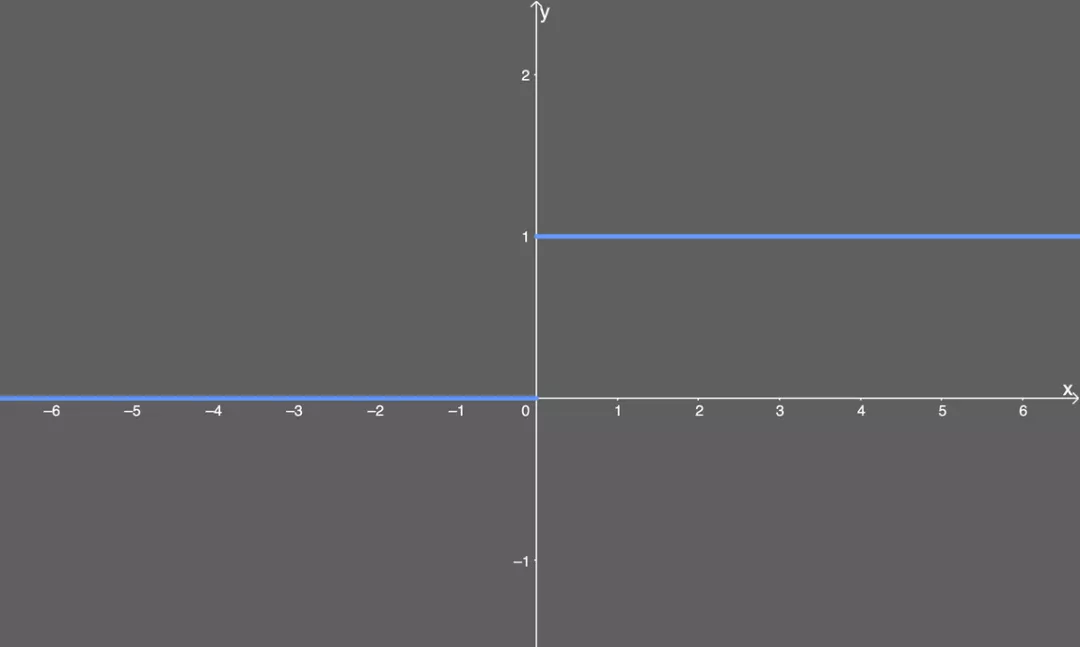
答案是：

当使用 ReLU 激活函数时，我们不会得到非常小的值（比如前面 sigmoid 函数得到的 0.0000000438），因为ReLU的导函数的值要么是 0（导致某些梯度不返回任何东西），要么是 1。

3.1 ReLU的缺点

【死亡ReLU问题】

从上面的解释可以得到，尽管通过ReLU避免了会得到很小的值，但是会引起另外一个很严重的问题：

当输入小于0的时候，会得到0更新。那么，可以想象，当如果输入存在较多的小于0的值时，这就会导致网络学习陷入了停滞的状态，网络不再更新。

3.2 ReLU特点总结

优点：

• 相比于Sigmoid，由于稀疏性，时间和空间复杂度更低，不涉及到过于复杂的指数运算；

• 避免了梯度消失的问题

缺点：

• 引入了死亡ReLU，即网络内的部分参数永远都不会更新了；（但有的时候也是一个优势）

• ReLU不能避免梯度爆炸的问题

问题4：ELU函数？

指数线性单元（ELU）：指数线性单元激活函数解决了 ReLU 的一些问题，同时也保留了一些好的方面。这种激活函数要选取一个 α 值；常见的取值是在 0.1 到 0.3 之间。

$$ELU(x)=\left\{\begin{align}\alpha (e^x - 1),x\le 0\\\\x,x > 0\end{align}\right.$$

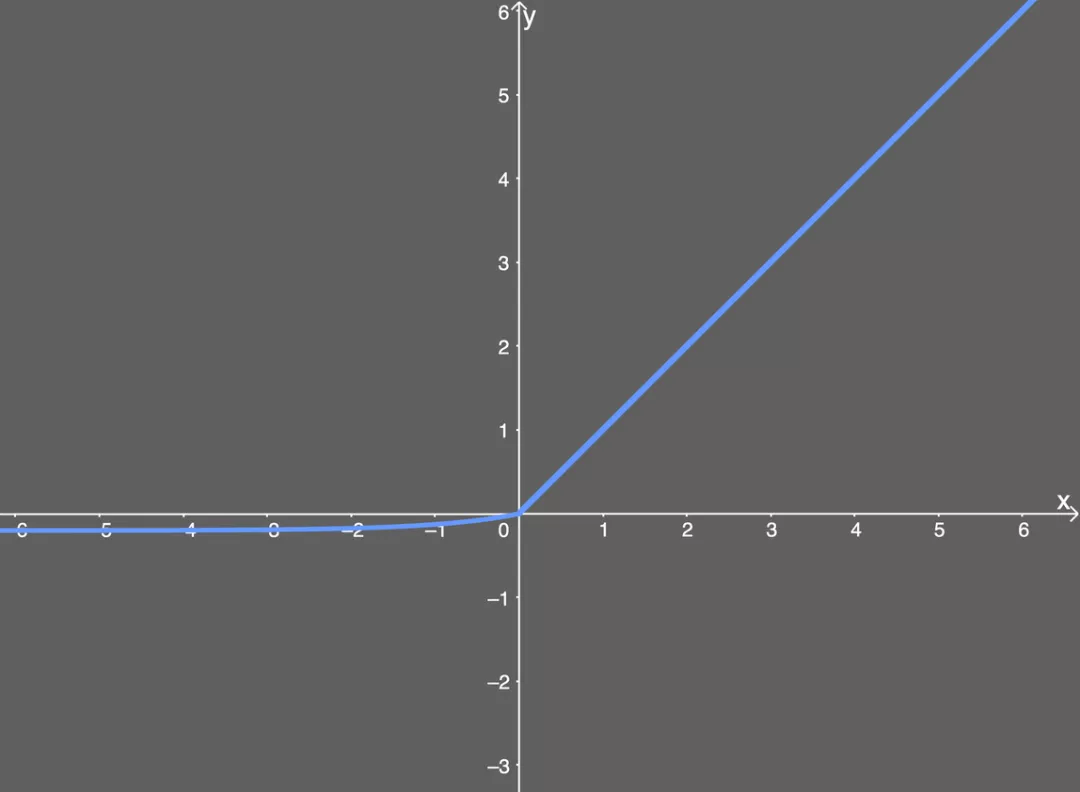
也就是说：如果输入的 x 值大于 0，则结果与 ReLU 一样——即 y 值等于 x 值；但如果输入的 x 值小于 0，则我们会得到一个稍微小于 0 的值。

4.1 ELU的导函数

$$ELU'(x)=\left\{\begin{align}\alpha + ELU(x),x\le 0\\\\1,x > 0\end{align}\right.$$

看起来很简单。如果输入 x 大于 0，则 y 值输出为 1；如果输入 x 小于或等于 0，则输出是 ELU 函数（未微分）加上 α 值。

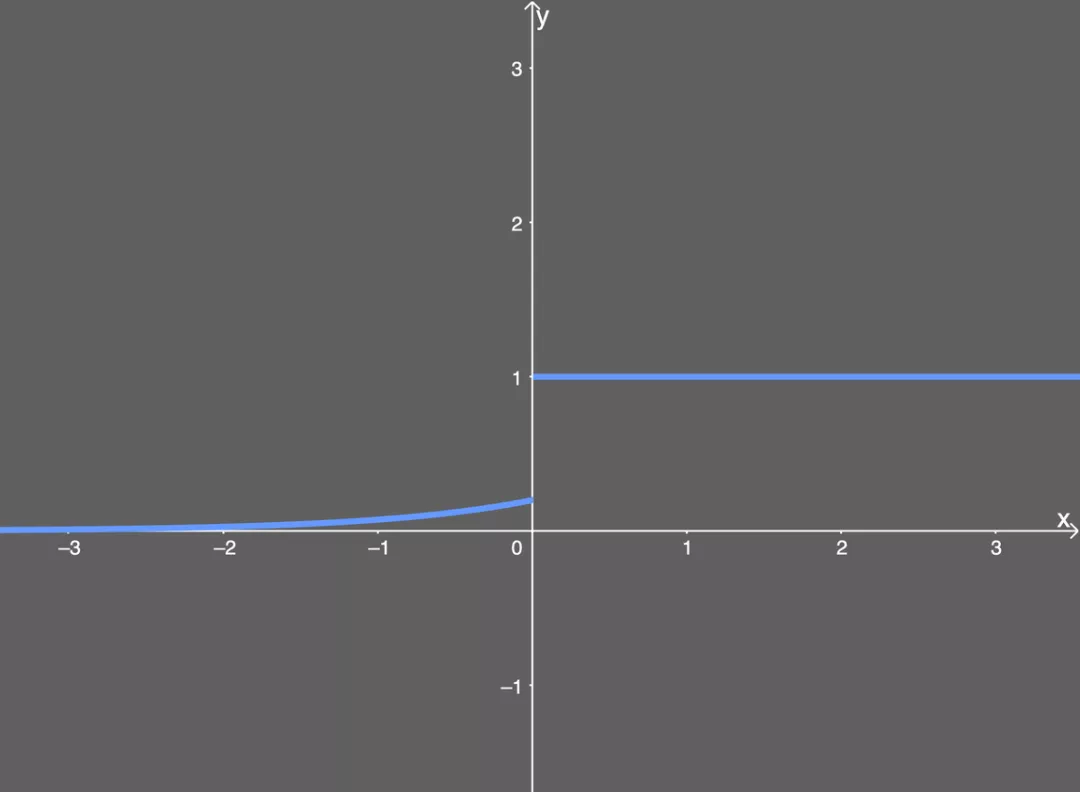
【闪光之处】：

从函数图上可以直观的看出来，成功的避免了死亡ReLU的问题，但与此同时又保持了ReLU 激活函数的一些计算速度增益——也就是说，网络中仍还有一些死亡的分量

4.2 ELU特点总结

优点：

• 能避免死亡 ReLU 问题，在计算梯度时能得到激活，而不是让它们等于 0；

• 能得到负值输出，这能帮助网络向正确的方向推动权重和偏置变化；

缺点：

• 由于包含指数运算，所以计算时间更长；

• 无法避免梯度爆炸问题；

• 神经网络不学习 α 值。

问题5：Leaky ReLU？

Leaky ReLU激活函数很常用，但相比于 ELU 它也有一些缺陷，但也比 ReLU 具有一些优势。

Leaky ReLU的数学形式如下：

$$LReLU(x)=\left\{\begin{align}\alpha x,x\le 0\\\\x,x > 0\end{align}\right.$$

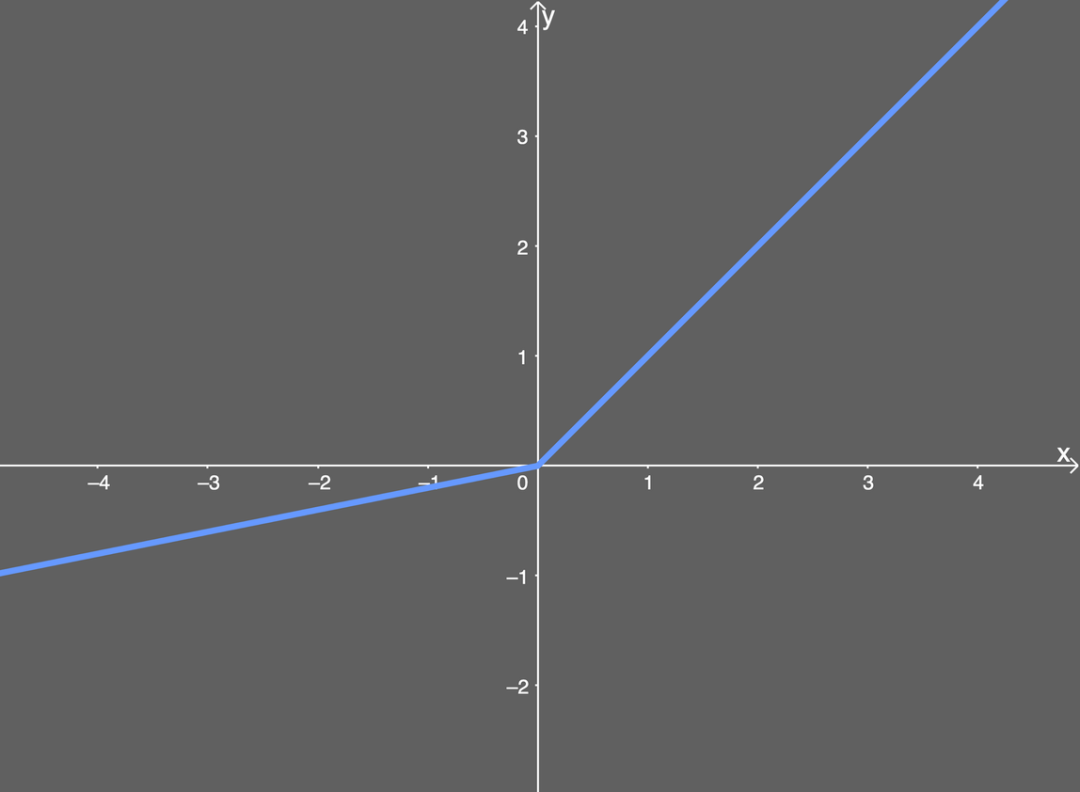
这里有一个参数值α，通常取值在0.1-0.3之间。这样的话，Leaky ReLU的微分值在输入 x 大于或小于 0时，各为一个常量（为正的时候，微分值为1；为负的时候，微分值为α）

5.1 Leaky ReLU特点总结

优点：

• Leaky ReLU能避免死亡 ReLU 问题，因为其在计算导数时，在输入为负时允许较小的梯度；

• 由于不包含指数运算，所以计算速度比 ELU 快。

缺点：

• 无法避免梯度爆炸问题；

• 神经网络不学习 α 值；

• 在微分时，两部分都是线性的；而 ELU 的一部分是线性的，一部分是非线性的。

问题6：GeLU函数？

在Transformer 模型（谷歌的 BERT 和 OpenAI 的 GPT-2）中得到了应用。GELU 的论文来自 2016 年，但直到最近才引起关注，下面论文是GELUs的第3版。

论文原文：GAUSSIAN ERROR LINEAR UNITS (GELUS)

6.1 Introduction

1. 以往的激活函数为神经网络进入了非线性（binary threshold, sigmoid, ReLU, ELU, 及特点和优劣）

2. 神经网络中需要在网络层中加入一些noise,或通过加入dropout等方式进行随机正则化。

3. 以往的非线性和随机正则化这两部分基本都是互不相关的，因为辅助非线性变换的那些随机正则化器是与输入无关的。

GELU的核心思想就是：将非线性与随机正则化结合。

6.2 GELU表达式

将Input x 乘以一个服从伯努利分布的m，而该伯努利分布又是依赖于输入Input x的。

这里X是选择标准正态分布的，原因是：一般神经元的输入数据的分布倾向于服从正态分布，尤其是进行了BatchNorm之后。

$$m\thicksim Bernoulli(\Phi(x)),\ where \ \Phi(x)=P(X\le x)$$

其中，X满足标准正态分布：

$$\Phi(x)=F(x;0,1)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^x e^{-\frac{t^2}{2}}dt$$

这样，GeLU的表示为：

$$GELU(x)=xP(X\le x)=x\Phi(x)$$

其中，用误差函数erf(x)表示标准正态分布：

$$\begin{align} \Phi(x)&=\frac{1}{2}+\frac{1}{2}erf\big(\frac{x}{\sqrt 2}\big)\\ \ \\ erf(x)&=\frac{1}{\sqrt\pi}\int_{-x}^x e^{-t^2}dt=\frac{2}{\sqrt\pi}\int_0^x e^{-t^2}dt \end{align}$$

因为erf项，无解析表达式，可以近似表示为：

$$erf(x)\approx \frac{2}{\sqrt \pi}tanh(x)$$

GELU的函数图像如下：

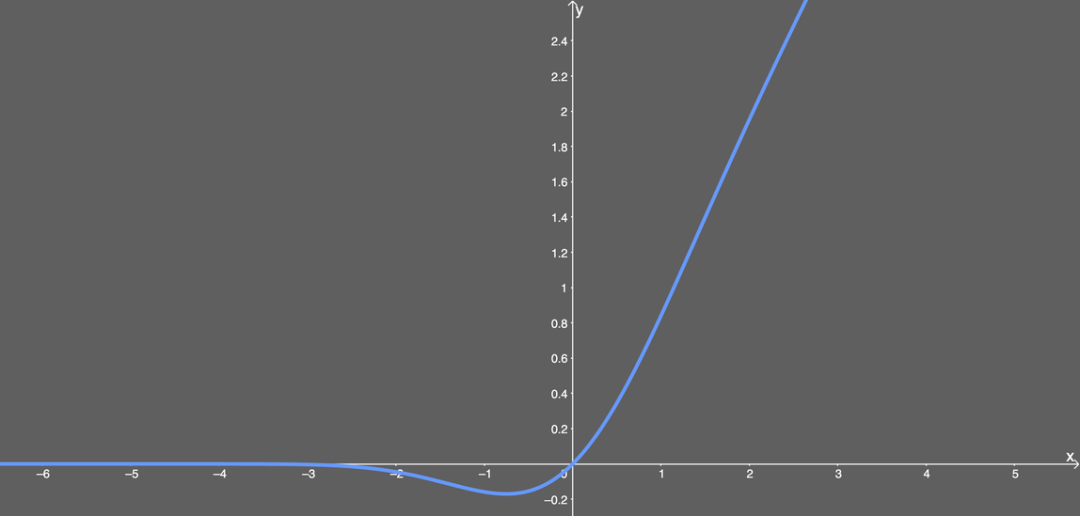
如何理解呢？

有一个服从正态分布的随机变量X，它不停歇的沿着钟形曲线走来走去。现在网络中有了 输入值 input 𝑥 = 𝑥0，就在此刻这个服从正态分布的随机变量取值为 X = X0，就可以比较 X0 与 𝑥0的大小了。

当X是服从正态分布的，我们可以依据该概率分布函数的特点，分析出一般情况下X有多大概率是小于某个确定值𝑥的。（比如P(X < 0.5) = 0.5）就得到了Φ(𝑥)。

正态分布的累积分布函数如下图。可以看出当𝑥变小时，P(X <= 𝑥)的值会减小，也就是当输入值inpuits 较小时，inputs被drop 的可能性更大。

GELU通过这种方式加mask，既保持了不确定性，又建立了与input的依赖关系。

bert源码给出的GELU代码表示如下：

def gelu(input_tensor):
    cdf = 0.5 * (1.0 + tf.erf(input_tensor / tf.sqrt(2.0)))
    return input_tesnsor*cdf

6.3 GELU与ReLU的区别？

• ReLU：为Inputs乘以一个0或者1，所乘的值是确定的，是依据Sign(x)来确定的；

• GELU：也会为Inputs乘以0或者1，GELU所加的0-1mask的值是随机的，同时是依赖于inputs的分布的。

这样做的好处是：（纯属个人理解）为ReLU更增加了随机性，同时又加强与Input之间的依赖关系。